背景介绍
字符串匹配是一个很常见的问题。
例如:判断文本字符串”BBC ABCDAB ABCDABCDABDE”里面是否包含另一个模式字符串”ABCDABD”。一般的思路很简单,只需要将两个字符串从头开始比较即可(分别使用i、j标识文本字符串和模式字符串的比较位置),若字符相同,则将两个字符串同时向后移一位(i++,j++);若不同,将文本串串回溯至初始比较位置的下一位(i=i-j+1),将模式串移动至头部(j=0),直到完全匹配或遍历完整个文本字符串。
上面的方法就是暴力匹配算法,但是这种简单粗暴的算法效率上存在着很大的问题,如上面提到的,当i=10,j=6时,字符串会失配,如下图
按照暴力匹配算法的话就会将模式串移到头部,文本串移到i=5的位置
这样做虽然可行,但是效率很差,因为你要把”搜索位置”(指针i)移到已经比较过的位置,重比一遍。当空格与D不匹配时,其实知道前面六个字符是”ABCDAB”,所以其实是没有必要将文本串回溯到i-j+1的位置的。
KMP算法
简述
KMP算法是由Donald Knuth、Vaughan Pratt、James H. Morris三人联合发表,作用就是查找文本串中是否包含特定的模式串。它的基本思想就是设法利用已知信息,不把”搜索位置”(指针i)移回已经比较过的位置,而是继续把它向后移,这样就会大大提高匹配效率。
下面我简述一下KMP算法的流程,
如果j = -1,或者当前字符匹配成功(即S[i] == P[j]),令i++,j++,继续匹配下一个字符;
如果j != -1,且当前字符匹配失败(即S[i] != P[j]),则令 i 不变,j = next[j]。此举意味着失配时,模式串P相对于文本串S向右移动了j - next [j] 位。
使用之前的例子的话就像下面这样
然后我们的问题就变成了模式串P应该向前移动多少位,即next[j]的值是什么。
next数组
由上面可知,那么next[j]就表示模式串中第j位失配后下一步需要移动到的位置,实际移动的位数为:j-next[j]。next数组和文本串是无关的,但是怎么求得next数组呢?
通过观察上面的例子我们可以看到,失配时移动到的位置k(也就是next[j])存在着这样一个性质:最前面的k个字符和j之前的最后k个字符是一样的。数学公式表示就像下面这样
P[0 ~ k-1] = P[j-k ~ j-1]
真前缀和真后缀的最大公共长度
所以我们要先求模式串中真前缀和真后缀的最大公共长度。
下面是关于(真)前缀后缀的定义(在阮一峰大佬的博客中混淆了前/后缀和真前/后缀的概念,看来大佬也有粗心的时候啊)。
下面是一个字符串“abab”的真前缀真后缀最大公共长度表
| 模式串 | a | b | a | b |
|---|---|---|---|---|
| 真前缀真后缀最大公共长度表 | -1 | 0 | 0 | 1 |
把初始值赋值为-1,可以方便匹配操作。
next数组的求解
重头戏终于来了,我们可以用递推的方法来求解next数组,如下图: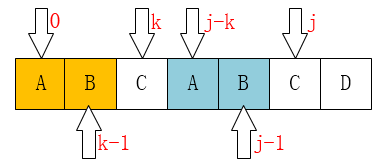
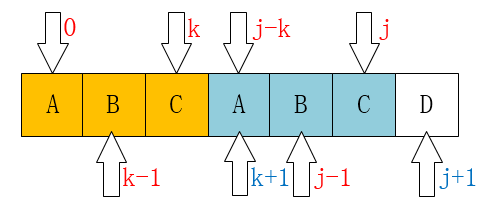
可以发现,
当P[k] == p[j]时,有next[j+1] = k+1.
关于这个结论证明如下:
已经知道P[0 ~ k-1] == P[j-k ~ j-1],并且P[k] == p[j]
所以P[0 ~ k] == P[j-k ~ j],即next[j+1] = k+1 = next[j]+1.
当P[k] != P[j]的时候呢,如图: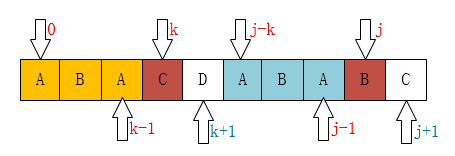
执行k=next[k],然后继续比较P[k]与P[j]。不停循环上面的步骤,直到P[k] == P[j]或者k=-1。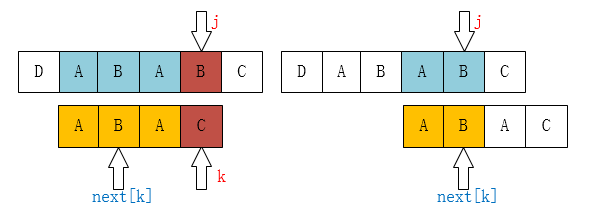
通过上面的图我们应该知道为什么使k=next[k],因为匹配不到”ABAAB”这样的串了,但是会有可能匹配到”AB”、”B”这样的串,此过程相当于模式串的自我匹配,所以不断的递归k = next[k],直到要么找到长度更短的相同前缀后缀,要么没有长度更短的相同前缀后缀。
这样我们就可以写出计算next数组的代码了
下面是KMP搜索的代码
Next数组的优化
表面上我们已经完成了所有工作,但是我们忽略了一个问题:
比如,如果用之前的next 数组方法求模式串“abab”的next 数组,可得其next 数组为-1 0 0 1,当它跟下图中的文本串去匹配的时候,发现b跟c失配,于是模式串右移j - next[j] = 3 - 1 =2位。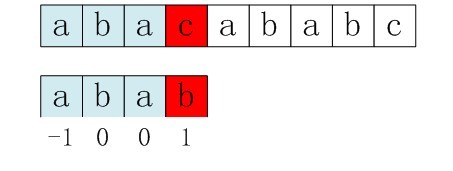
右移2位后,b又跟c失配。事实上,因为在上一步的匹配中,已经得知p[3] = b,与s[3] = c失配,而右移两位之后,让p[ next[3] ] = p[1] = b 再跟s[3]匹配时,必然失配。问题出在哪呢?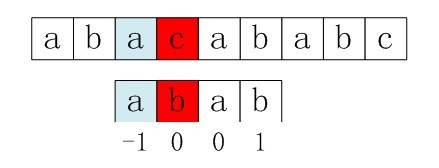
问题出在不该出现p[j] = p[ next[j] ]。为什么呢?理由是:当p[j] != s[i] 时,下次匹配必然是p[ next [j]] 跟s[i]匹配,如果p[j] = p[ next[j] ],必然导致后一步匹配失败(因为p[j]已经跟s[i]失配,然后你还用跟p[j]等同的值p[next[j]]去跟s[i]匹配,很显然,必然失配),所以不能允许p[j] = p[ next[j ]]。如果出现了p[j] = p[ next[j] ]咋办呢?如果出现了,则需要再次递归,即令next[j] = next[ next[j] ]。
修改后的代码如下: